
In the above circuit diagram one of the XOR gate from 74LS86 is used and also one of the AND gate from 74LS08 is used.
We constructed the circuit in breadboard and observed the output. These two ICs are widely available and we will make Half-Adder circuit using this two.īelow is the Pin Diagram for both the ICs:Ĭircuit Diagram to use these two ICs as a half-adder circuit. 74LS86 has four XOR gates inside the chip and 74LS08 has four AND gates inside it.

#Half adder truth table series#
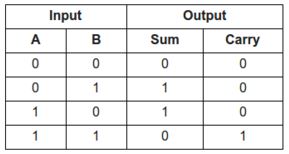
For this we used two widely used XOR and AND chip from 74 series 74LS86 and 74LS08.īoth are gate ICs. We can make the circuit in real on breadboard to understand it clearly. Practical Demonstration of Half Adder Circuit: Truth table of Half-Adder circuit is as follows. The Boolean expression of Half Adder circuit is- SUM = A XOR B (A+B) CARRY = A AND B (A.B) This is the construction of Half-Adder circuit, as we can see two gates are combined and the same input A and B are provided in both gates and we get the SUM output across EX-OR gate and the Carry Out bit across AND gate. So the Half-Adder logical circuit can be made by combining this two gates and providing the same input in both gates. In the above, the truth table of AND gate is shown where it will only produce the output when both inputs are 1, Otherwise it will not provide an output if both inputs are 0 or any of the inputs is 1. The output is depends on the AND gate truth table. If we provide A and B bit in the input it will produce an Output. Same as like EX-OR gate it has two inputs. This is the basic circuit of two input AND gate. AND gate is perfectly fits in this application. X-OR gate only provides the sum and unable to provide carry bit on 1 + 1, we need another gate for Carry. On the two other cases when both inputs are 0 or 1 the Ex-OR gate produce 0 outputs. When any one of the bits A and B is 1 the output of the gate becomes 1. In the above table we can see the total sum output of the EX-OR gate. The truth table of EX-OR gate is – Input A A, and B is the two binary input and SUMOUT is the final output after adding two numbers. This is the symbol of two inputs EX-OR gate. The Ex-OR gate is used to produce the SUM bit and AND Gate produce the carry bit of the same input A and B. 2-input Exclusive-OR Gate or Ex-OR Gate.We can make this circuit using two basic gates We have seen the Block Diagram of Half Adder circuit above with two inputs A,B and two outputs- Sum, Carry Out. So, if we see the operation of an adder circuit, we need only two inputs and it will produce two outputs, one is addition result, denoted as SUM and other one is CARRY OUT bit. In the first three row 0 + 0, 0 + 1 or 1+ 0 the addition is 0 or 1 but there is no carry bit, But in the last row we added 1 + 1 and it is produce a carry bit of 1 along with result 0. The first digit, we can denote as A and the second digit we can denote as B, are added together and we can see the summation result and carry bit. Let’s see possible binary addition of two bits, 1 st Bit or Digit We also use some ICs to practically demonstrate the Half Adder circuit.īelow is the block diagram of a Half-Adder, which requires only two inputs and provide two outputs.
#Half adder truth table full#
In this tutorial we will focus on Half Adder circuit and in next Tutorial we will cover Full adder circuit. We can also add multiple bits binary numbers by cascading the full adder circuits.
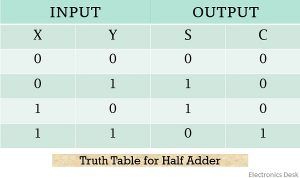
But in Full Adder Circuit we can add carry in bit along with the two binary numbers. In half adder we can add 2-bit binary numbers but we cant add carry bit in half adder along with the two binary numbers. Mainly there are two types of Adder: Half Adder and Full Adder. As in binary number system, 1 is the largest digit, we only produce carry when the addition is equal or greater than 1 + 1 and due to this, carry bit will be passed over next column for addition. These two numbers can represent SUM or CARRY or both. In binary, we only get two numbers either 1 or 0. Instead of the two denary numbers here binary numbers are used.
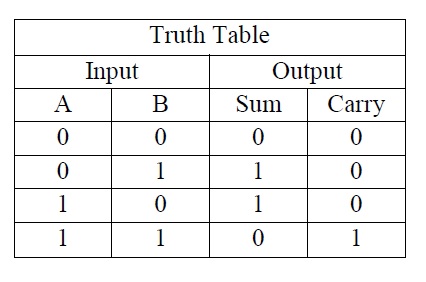
In case of binary number addition the process is same. So, each value has a weighted value based on its column position. We wrote 0 and carry the 1 to the next column. We add each column from right to left and if the addition greater than or equal to 10, we use carry.


 0 kommentar(er)
0 kommentar(er)
